I love using k-fold cross validation for my machine learning projects. But especially when I am dealing with neural network models that take hours or even days to train doing a full k-folds style analysis becomes an uncomfortably heavy computational burden. Unfortunately for models with such long training times I usually abandon training an esemble of models and just train one model with a single train/validation split.

I really wanted a way to get at least some of the diagnostic benefits you get from having an ensemble of semi-independently trained models the way you do in K-folds, but without needing to wait days or weeks for my neural nets to train. I started experimenting with weakly coupled mixtures of models. Instead of feeding most of the data to K otherwise independent models as in K-folds why not try feeding just a fraction 1/K of the data to each model and let the models communicate about their parameters with each other in a controlled way. I thought that perhaps by cleverly controlling what information is passed between which models, how often messages are passed, and how information from them may be used I could effectively isolate the information in some data folds from the values of the parameters of some of the models. In this way I could hopefully save some computation time over a k-folds cross validation without sacrificing all of its benefits.

K-Fold Cross Validation

First off, lets talk about cross validation using K-folds. In a K-fold cross validation scheme you split your data into K different data sets of roughly equal sizes. Each of these data sets is a data fold. In order to get an idea of how well your model will do when operating on unseen data you train each of your models on a large subset of all the data but leaving out one of the data folds. For convenience suppose you leave fold 1 out when training model 1, fold 2 is left out when training model 2, etc. Then the performance of model 1 on the data in fold 1 will give a robust estimate of the performance you can expect from your model on previously unseen data.

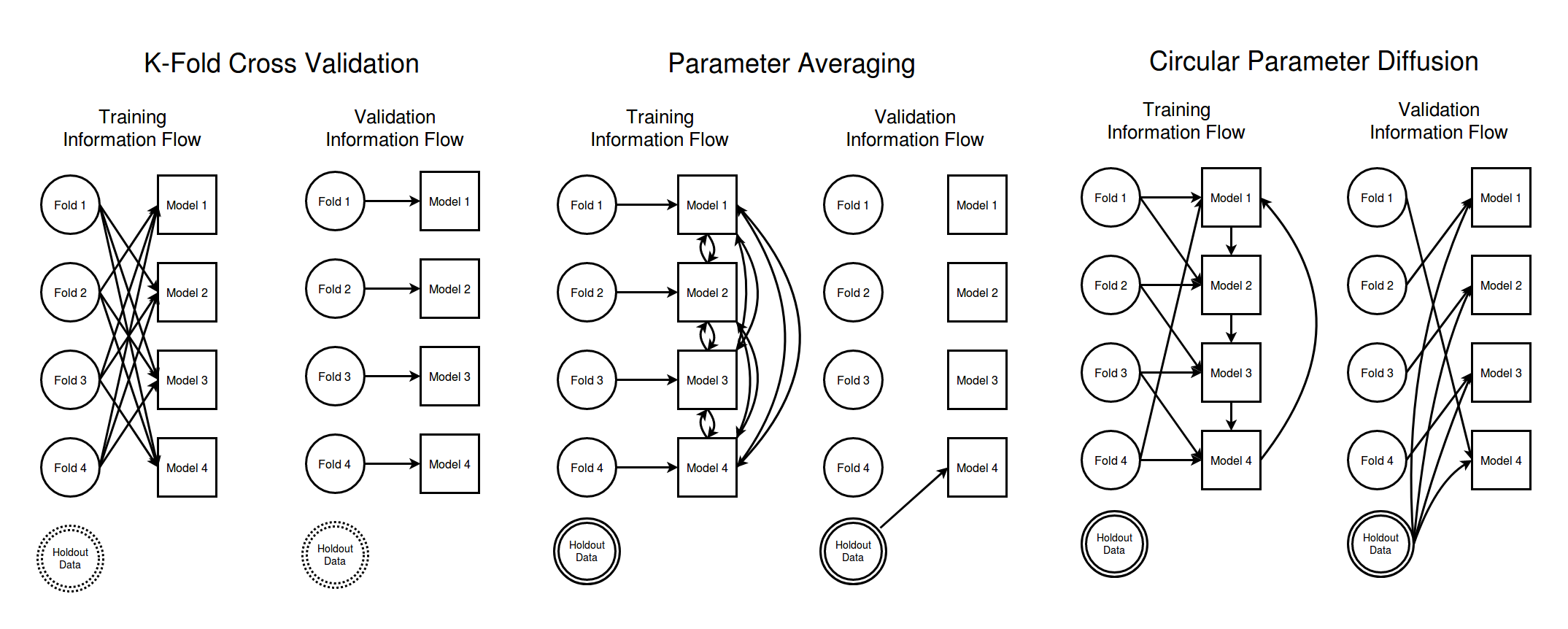
To help visualize how the flow of information is controlled in a k-fold cross validation analysis I have made a diagram showing the information flow for a situation with 4 data folds. The left column shows how information flows during the training of the models and the right column of the diagram shows how information flows as we are validating our model quality. The circles represent data sets broken up into independent folds and I have drawn an arrow from a data set to a model if the model is allowed to use that data set.

The "hold out data" node in the above diagram is not really necessary for K-folds since thanks to the fact that there is no training time path from data set $i$ to model $i$ the different training folds are our hold out validation sets. I have included the hold out data node in order to keep the diagrams consistent for all the methods we will consider.

Distributed Parameter Averaging

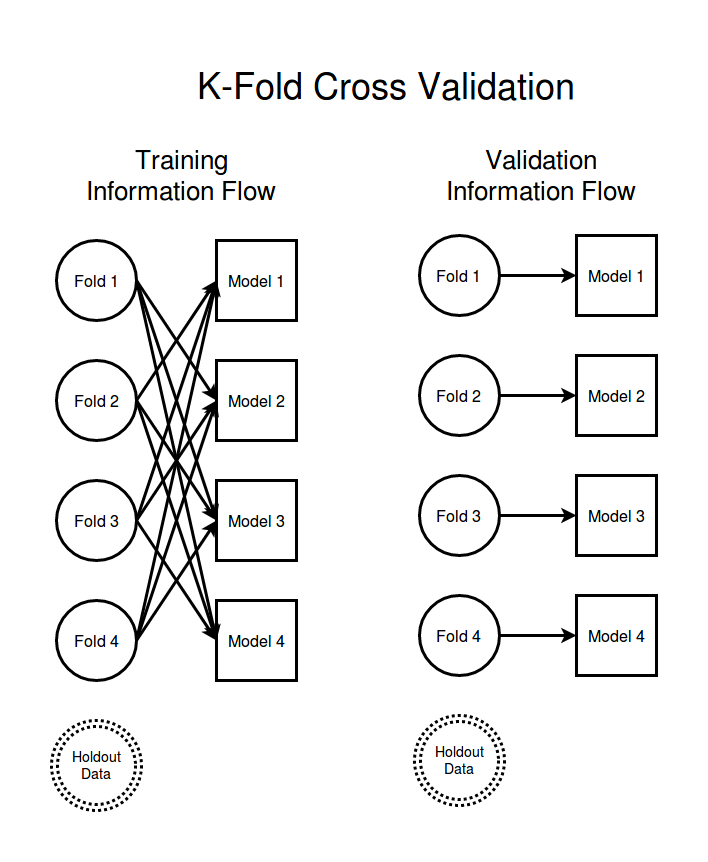
Now lets consider a very different sort of information handling strategy. Instead of giving each model access to most of the data we give each model access to only one data fold. If we didn't then allow the individual models to communicate with each other then we would get an ensemble of K independent but probably very weak models. But if we let the models communicate about their parameters with each other then the different models can come to a consensus about the best set of parameters. When the goal of the communication between models is to keep each models parameters as close as possible to the parameters of the other models this is a distributed training strategy called parameter averaging. Visualizing the flow of information in a parameter averaging scheme you get the following,

Note that the arrows running between data nodes and models and the arrows running betwen models indicate very different sorts of communication. In the case of arrows from data to models the information being passed is the data itself (or possibly the gradients with respect to the current model parameters induced by that data). In the case of parameter averaging the model to model arrows represent an exchange of model parameter values. The way that parameter averaging is typically executed is by having one copy of the model living on each of K compute nodes each with just its part of the training data. A special "parameter server" node constantly collects, averages, and redistributes the parameters of each training node with the goal being to keep the different models parameters as similar to each other as possible. I have represented this operation here by a dense connection of arrows in both directions between all the models, since every model both receives and transmits information about its parameters to every other model with every averaging step.

If you don't keep the parameters of each model extremely similar to each other the gradients obtained by each model start to diverge from each other and simply taking the average of the different model parameters after a large number of training iterations doesn't work very well This is because of the very non-linear nature of the models being trained. If you take the mid-point parameters of two linear models then the resulting model gives predictions which are the average of the individual predictions. For complex non-linear models the mid-point parameters of two models can't be expected to give anything like the average of the predictions. The more different the parameters are from each other the less the mid-point parameters will act like an average prediction and the more damaging to model quality the averaging step is.

Because of the necessity to keep the parameters of the different models as tightly coupled together as possible parameter averaging is not usually thought of as an esemble method but instead is simply a way to leverage a large number of compute nodes to simultaneously train a single model. Looking at the information flow network above it is easy to see that there is no reasonable way to treat any data fold as being a good validation set for any model and so it is essential that we keep a separate hold out set to validate our model quality with. Since the goal of frequent and every-to-every parameter broadcasting is to keep all the models as similar as possible to each other we can simply pick one of the models and use it to evaluate the model quality on the hold out set. Thus the single arrow from hold out to the last model in the above diagram.

Circular Parameter Diffusion (CPD)

Looking at the above diagrams of K-fold cross validation and distributed parameter averaging I think it is pretty clear that the two algorithms represent nearly polar opposite strategies of information flow. The K-folds has a densely connected data to model information flow but no model communication at all, parameter averaging has no direct data sharing but depends on dense and frequent communication between all the models. Let's take a mid ground which has some of the data insulating properties of K-folds but also allows for some limited communication between models.

The goal of the K-fold style of information flow is to hide some information from some models but because there is no communication between the different models there is no sharing of the computational burden between different models and so training the ensemble is very computationally expensive. On the other hand the goal of parameter averaging is to use the available compute power as efficiently to compute a single model very fast. As a result there is no advantage gained from having an ensemble of models and no model can be considered even remotely independent of any piece of data forcing us to rely entirely on a hold out set for model quality control.

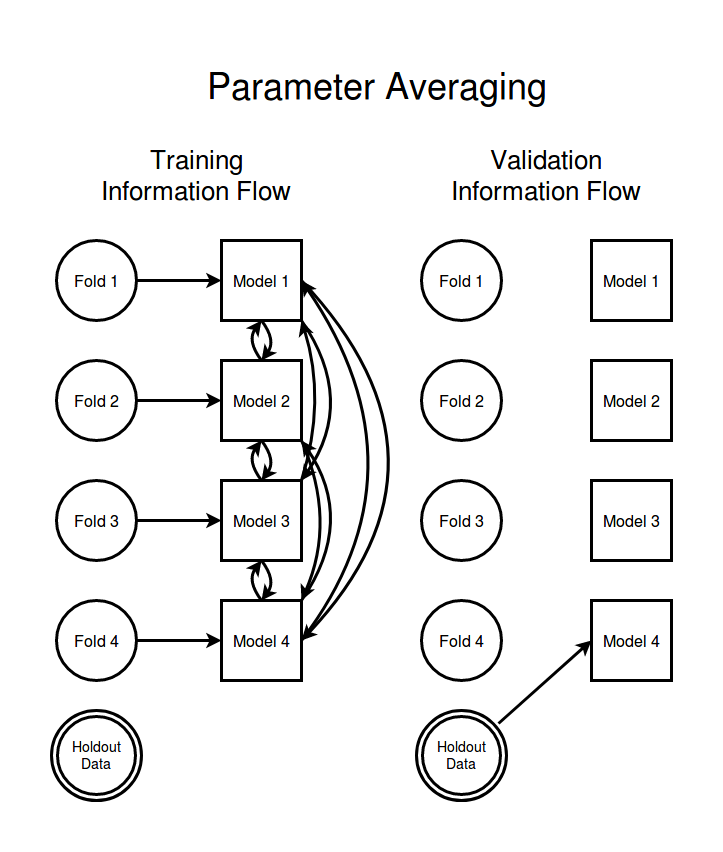
Let's allow some message passing between models so that the models can help each other to train more efficiently like in parameter averaging but we still tried to insulate some models from the data held in some data folds. Ideally we would like to get a model training technique that is fast like parameter averaging but which maintains some of the extra diagnostic power that comes with having a true ensemble of different models. Instead of using a densely connected 2-way communication channel between models during training we just pass parameters one way, and instead of densely connecting the models we just let each model talk to only a single other model. The natural information flow structure is to connect the models together in a message passing loop.

The two way arrows in the parameter averaging scheme represented replacing the model parameters with the average of the connected models. What do these one way arrows in circular parameter diffusion represent? At intervals we send a message from one model to the next consisting of the parameters of that model. Instead of replacing the current parameters with an unweighted average of the two parameter sets we take a small step towards the parameters of the informant model. The size of the step we take is controlled by a mixing strength parameter $\alpha$.

$$ \theta_{t+1, i} = (1-\alpha) \theta_{t, i} + \alpha \theta_{t, i+1} $$

I have been calling this a "diffusion update" since after many such updates the effects of the parameters of each model slowly diffuse through the entire ensemble. The $\alpha$ parameter may be thought of as a learning rate for the diffusion updates. With a low value for $\alpha$ even if the differences between the parameters of different models are fairly large the updates from the diffusion step will still represent small perturbations. The reason to keep $alpha$ small is entirely analogous to the reason that it is good to use a low learning rate with gradient descent. A high learning rate may facilitate quicker learning but also runs the risk of taking steps which are too large for the gradient to be a good representation of the structure of the function. In the case of the diffusion steps if the informant models parameters differ significantly from the target models parameters then moving to the midpoint parameters may cause too much disruption to the model. By keeping $\alpha$ small any one diffusion update is likely to be just a small perturbation and so will not disrupt the target model much. If $\alpha$ is low then the communication between models is weak and it may take many many averaging steps for the models to effectively learn from each other. But keeping our step sizes small allows us to cope effectively with the non-linearity of the approximated function.

Because the diffusion step as we have defined it is asymmetric with each model being informed only by the models upstream from it that means that it will take quite a number of diffusion steps for the effects of certain data sets to diffuse far enough to affect the parameters of models far away in the model chain. For example the parameters of model 1 will take at least K-1 diffusion steps before they could even in principle begin affecting the parameters of model K. Keeping the diffusion learning rate $\alpha$ low also means that even after we have done perhaps many hundreds of diffusion steps the data in fold $i-1$ and the parameters of model $i$ may still not be meaningfully coupled together. This allows us to mimic the data isolating properties of K-folds without having to train each model completely independently.

However we can't be really certain that the parameters of any one model are effectively independent of any of our input data. It may take a lot of diffusion steps but eventually we must expect that the parameters of all our models will come to be dependent on the data in every fold, regardless of how many models lie between them or how small our diffusion coupling $\alpha$. Therefore it is still a good idea to keep a small independent hold out data set which we never feed in to any of our models during training.

I would think that one could could treat a small holdout set as a sort of canary. As long as the model quality estimates of the hold out set roughly match the model quality estimates obtained by pairing data fold $i$ with model $i-1$ we can assume that the later is still a valid model quality estimate. This allows us to treat a circular parameter diffusion model ensemble in much the same way as we would treat a K-folds ensemble giving us the benefit of a low variance model quality estimate (albeit one with a bias that may increase over time).

Fashion MNIST test Case

Now lets put these ideas to the test and see how circular parameter diffusion performs on a real data set in comparison to training a single monolithic model or training an ensemble via K-folds. I want a dataset which is just a bit more challenging than MNIST but which I can still train models for quickly. I've decided to use the fashion MNIST data set. Fashion MNIST is significantly harder to do well on than MNIST, in the table 3 of the fashion MNIST announcement paper they list a large number of machine learning algorithms and their respective accuracies on Fashion MNIST and MNIST. MNIST has a large number of models which achieve around 97% accuracy whereas on fashion MNIST none of the benchmark models perform at even 90% accuracy.

Importantly essentially linear models like logistic regression actually do a pretty good job on MNIST data getting over 90% while they get closer to 80% on fashion MNIST. Parameter averaging in linear models is an intrinsically more stable process than parameter averaging on non-linear models. The higher degree of non-linearity which we are forced to deal with if we wish to achieve a high accuracy on the fashion MNIST data will make it a better test case for

There are several questions which we will try to tackle,

• Does CPD train an ensemble of models faster than a K-folds arrangement?
• Can we take the average parameters of the CPD ensemble after training to boost performance?
• Are the CPD trained models as accurate as the K-folds models?
• Does CPD effectively isolate some data from the parameters of some models?
• Is a CPD based cross validation an effective estimate of our model accuracy?

import time
import numpy as np
np.random.seed(4321)
import pandas as pd

import scipy
import scipy.stats
import scipy.ndimage
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams.update(
    {
        "figure.figsize":(12, 6),
        "font.size":15,
        "image.cmap":"viridis",
        "image.aspect":"auto",
        "lines.linewidth":2,
    }
)

import tensorflow as tf
import keras

Using TensorFlow backend.

Train/Test Split

Instead of using the usual 60,000/10,000 train/test split of the data we will use only a small fraction of the data for training and use most of the data for the test set. This way the model accuracy estimate that we get from the test set will be more accurate than the estimate we get from the K-fold cross validation. This way not only will comparison with the test set give us a good idea of the accuracy of our models but will be accurate enough that we can treat the difference between the cross validation estimated accuracies and the test accuracy as the error in the cross validation estimated model accuracy.

n_train = 20000
batch_size = 32

#load the data
from keras.datasets import fashion_mnist as dset

(x_train, y_train), (x_test, y_test) = dset.load_data()

y_train = y_train.squeeze()
y_test = y_test.squeeze()

#stack train and test together
x_all = np.vstack([x_train, x_test])
y_all = np.hstack([y_train, y_test])

def normalize_images(
    im_arr,
):
    im_arr = im_arr.astype(float)
    flat_ims = im_arr.reshape((-1, np.prod(im_arr.shape[1:])))
    norms = np.std(flat_ims, axis=1)
    means = np.mean(flat_ims, axis=1)
    bcast_shape = [-1] + (len(im_arr.shape)-1)*[1]
    return (im_arr-means.reshape((bcast_shape)))/norms.reshape(bcast_shape)

x_all = normalize_images(x_all)

x_train = x_all[:n_train]
x_test = x_all[n_train:]

y_train = y_all[:n_train]
y_test = y_all[n_train:]

n_categories = len(np.unique(y_train))
y_train_onehot = keras.utils.to_categorical(y_train, n_categories)
y_test_onehot = keras.utils.to_categorical(y_test, n_categories)

Implementation

I have made a convenience wrapper which takes a compiled keras model and a list of the training data id's and then treats the model like an ensemble. The wrapper manages splitting the training data up into different data streams for each model and keeping around the different parameters for each model as well as the different parameters for the optimizers of each model. If you don't also remember to retrieve and set the parameters of the optimizers then you get some combination of poor or confusing performance (the one exception being pure SGD with no momentum since there is no optimizer state to speak of). I have stayed away from any optimizers which have some concept of momentum in the preparation of this post because there is no convenient way to incorporate the information from the diffusion updates into the momentum vector for the different models and I would be afraid of causing runaway feedback loops between the momentum and diffusion updates. I have experienced this sort of thing in the past when doing updates by hand in the middle of optimization with optimizers like ADAM. I have chosen to use adadelta because it is my usual go to optimizer and it seems to train these models very effectively.

Instead of actually making K different copies of each model we will make just 1 keras base model and periodically read and set the values of the model parameters. All this reading and writing to the parameter variables puts a strain on input/output bandwidth of the GPU. In order to stop all this I/O from slowing the training performance too much we need to do several gradient updates between parameter reads.

For convenience so that we can use the same CPD ensemble wrapper to implement K-folds training of our model I have also added a flag for turning off the diffusion updates.

def accumulate_from_stream(model, stream):
    accum_y = []
    accum_pred = []
    
    for batch in stream:
        ypred = model.predict(batch["x"])
        accum_y.append(batch["y"])
        accum_pred.append(ypred)
    
    return np.vstack(accum_y), np.vstack(accum_pred) 

class CircularDiffusionMetaModel(object):
    
    def __init__(
        self,
        model,
        source_identifiers,
        batcher_factory,
        train_stream_kwargs,
        validation_stream_kwargs,
        n_folds,
        k_overlap=0,
        iterations_per_round=10,
        mixing_alpha=0.01,
        diffusion_on=True,
        start_parameters=None,
        initial_dispersion=0.01,
        fold_seed=None,
        perturbation_seed=None,
    ):
        self.model = model
        self.n_folds = n_folds
        self.source_identifiers = np.array(source_identifiers)
        
        assert 0.0 <= mixing_alpha <= 1.0
        self.mixing_alpha = mixing_alpha
        self.iterations_per_round = iterations_per_round
        self.k_overlap = k_overlap
        self.diffusion_on = diffusion_on
        
        if fold_seed is None:
            fold_seed = int(np.random.random()*10000)
        
        if perturbation_seed is None:
            perturbation_seed = int(np.random.random()*10000)
        
        n_train = len(source_identifiers)
        
        fold_rstate = np.random.RandomState(seed=fold_seed)
        data_permutation = fold_rstate.permutation(n_train)
        
        train_identifiers = self.source_identifiers[data_permutation]
        split_indexes = np.linspace(0, n_train, n_folds+1)[1:-1].astype(int)
        split_train_ids = np.split(train_identifiers, split_indexes)
        assert len(split_train_ids) == self.n_folds
        
        train_streams = []
        fold_streams = []
        
        for fold_idx in range(n_folds):
            collected_ids = [split_train_ids[fold_idx]]
            for off_k in range(1, k_overlap+1):
                collected_ids.append(split_train_ids[(fold_idx-off_k)%self.n_folds])
            cur_train_batcher = batcher_factory(np.hstack(collected_ids))
            cur_fold_batcher = neurad.pipeline.FixedBatcher(split_train_ids[fold_idx])
            
            cur_train_stream = neurad.pipeline.DataStream(
                cur_train_batcher,
                **train_stream_kwargs,
            )
            
            cur_fold_stream = neurad.pipeline.DataStream(
                cur_fold_batcher,
                **validation_stream_kwargs
            )
            
            train_streams.append(cur_train_stream)
            fold_streams.append(cur_fold_stream)
        
        self.training_streams = train_streams
        self.fold_streams = fold_streams
        
        if start_parameters is None:
            start_parameters = model.get_weights()
        
        model_parameters = []
        optimizer_parameters = []
        
        perturb_rstate = np.random.RandomState(seed=perturbation_seed)
        
        for i in range(n_folds):
            fluctuated_params = []
            for param_idx in range(len(start_parameters)):
                cparam = start_parameters[param_idx].copy()
                cparam_delta = initial_dispersion*perturb_rstate.normal(size=cparam.shape)*np.std(cparam)
                fluctuated_params.append(cparam + cparam_delta) 
            model_parameters.append(fluctuated_params)
            optimizer_parameters.append(model.optimizer.get_weights())
        
        self.model_parameters = model_parameters
        self.optimizer_parameters = optimizer_parameters
        
        self.n_diffusion_steps = 0
        self.n_gradient_steps = 0
    
    def get_average_parameters(self,):
        mod_params = []
        n_params = len(self.model_parameters[0])
        
        for param_idx in range(n_params):
            avg_param = np.zeros(self.model_parameters[0][param_idx].shape)
            for fold_idx in range(self.n_folds):
                avg_param += self.model_parameters[fold_idx][param_idx]
            avg_param /= self.n_folds
            mod_params.append(avg_param)
        return mod_params
    
    def apply_diffusion(self):
        alpha = self.mixing_alpha
        new_fold_model_params = []
        for fold_idx in range(self.n_folds):
            current_fold = fold_idx
            informant_fold = (fold_idx + 1) % self.n_folds
            pset_current = self.model_parameters[current_fold]
            pset_informant = self.model_parameters[informant_fold]
            p_next = []
            n_params = len(pset_current)
            for param_idx in range(n_params):
                pv1 = pset_current[param_idx]
                pv2 = pset_informant[param_idx]
                mixed = pv1*(1.0-alpha) + pv2*alpha
                p_next.append(mixed)
            new_fold_model_params.append(p_next)
        
        self.model_parameters = new_fold_model_params
        self.n_diffusion_steps += 1
    
    def accuracy_on_stream(self, dstream, parameters="average"):
        if parameters == "average":
            self.model.set_weights(self.get_average_parameters())
        elif isinstance(parameters, int):
            self.model.set_weights(self.model_parameters[parameters])
        else:
            raise ValueError("parameters argument value not understood")
        
        y_true, y_pred = accumulate_from_stream(self.model, dstream)
        acc = np.mean(np.argmax(y_true, axis=1) == np.argmax(y_pred, axis=1))
        return acc
    
    def run_training_round(
        self,
    ):
        """Perform one round of training for all the models doing iterations_per_round gradient steps for each"""
        for fold_idx in range(self.n_folds):
            #load the parameters
            c_mod_params = self.model_parameters[fold_idx]
            c_opt_params = self.optimizer_parameters[fold_idx]
            self.model.set_weights(c_mod_params)
            self.model.optimizer.set_weights(c_opt_params)
            
            dstream = self.training_streams[fold_idx]
            for batch_idx in range(self.iterations_per_round):
                cbatch = dstream.get_batch()
                self.model.train_on_batch(cbatch["x"], cbatch["y"])
            
            self.model_parameters[fold_idx] = self.model.get_weights()
            self.optimizer_parameters[fold_idx] = self.model.optimizer.get_weights()
        
        self.n_gradient_steps += self.iterations_per_round
        if self.diffusion_on:
            self.apply_diffusion()
    
    def timed_training_run(
        self,
        train_duration,
    ):
        stime = time.time()
        
        while time.time()-stime < train_duration:
            self.run_training_round()

Model Architecture

Since I am using just a small portion of the total training data I don't want to use a model with so many model parameters that my models immediately overfit. This is particularly true since we are using only a small part of the available training data. But I also wanted to make sure that the model is deep enough to make a good stress test of the diffusion type updates (the idea being that deeper networks are more non-linear).

In the end most of the model architectures I tried out performed very similarly whether they had 5 layers or 8 layers and whether they had a million parameters or 250,000. The model below is on the smaller side of the models that I played with in terms of numbers of free parameters but is on the larger side in terms of number of layers.

from keras.layers import Conv2D, MaxPooling2D, Dense, Lambda
from keras.layers import BatchNormalization, Flatten, Dropout
from keras.layers import SeparableConv2D, concatenate

im_size = x_train.shape[1:]

def make_network(
    dropout_rate,
    inner_activation,
    im_size,
):
    x_in = keras.layers.Input(im_size)
    x = x_in
    
    if len(im_size) == 2:
        x = keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=3))(x)
    
    x = Conv2D(32, (3,3), padding="same", activation=inner_activation)(x)
    x = Conv2D(64, (3,3), padding="same", activation=inner_activation)(x)
    x = MaxPooling2D(pool_size=2, strides=2, padding="same")(x)
    x = Conv2D(128, (3,3), padding="same", activation=inner_activation)(x)
    x = MaxPooling2D(pool_size=2, strides=2, padding="same")(x)
    x = Conv2D(128, (2, 2), padding="same", activation=inner_activation)(x)
    x = Conv2D(16, (1, 1), padding="same", activation=inner_activation)(x)
    
    x = Flatten()(x)
    
    x = keras.layers.Dropout(dropout_rate)(x)
    
    x = Dense(100, activation=inner_activation)(x)
    x = Dense(100, activation=inner_activation)(x)
    
    probs = Dense(10, activation="softmax")(x)
    return keras.models.Model(x_in, probs)

model_kwargs = dict(
    dropout_rate=0.4,
    inner_activation="relu",
    im_size=im_size,
)

base_model = make_network(**model_kwargs)
base_model.compile(loss="categorical_crossentropy", optimizer="adadelta", metrics=["accuracy"])

base_model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 28, 28)            0         
_________________________________________________________________
lambda_1 (Lambda)            (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 28, 28, 32)        320       
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 28, 28, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 64)        0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 14, 14, 128)       73856     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 7, 7, 128)         0         
_________________________________________________________________
conv2d_4 (Conv2D)            (None, 7, 7, 128)         65664     
_________________________________________________________________
conv2d_5 (Conv2D)            (None, 7, 7, 16)          2064      
_________________________________________________________________
flatten_1 (Flatten)          (None, 784)               0         
_________________________________________________________________
dropout_1 (Dropout)          (None, 784)               0         
_________________________________________________________________
dense_1 (Dense)              (None, 100)               78500     
_________________________________________________________________
dense_2 (Dense)              (None, 100)               10100     
_________________________________________________________________
dense_3 (Dense)              (None, 10)                1010      
=================================================================
Total params: 250,010
Trainable params: 250,010
Non-trainable params: 0
_________________________________________________________________

In order to do a fair comparison between the various different training techniques it is important that we start all the ensembles off centered around the same initial parameters. In order to do that we can just fetch the weights of our base model and feed them in as the starting parameters for all our ensembles.

start_parameters = base_model.get_weights()

import neurad as nrd
import neurad.pipeline

class NumpyArrayTransformWrapper(object):
    
    def __init__(
        self, 
        data_arr,
        output_key,
        as_array=True,
    ):
        self.data_arr = data_arr
        self.output_key = output_key
    
    def __call__(self, data_in):
        indexes = data_in["id"]
        targ = self.data_arr[indexes]
        
        #put the extracted data back into the data dictionary and return the whole dictionary
        data_in[self.output_key] = targ
        
        return data_in

train_transformer = neurad.pipeline.DataTransformer(
    [
        NumpyArrayTransformWrapper(x_train, output_key="x"),
        NumpyArrayTransformWrapper(y_train_onehot, output_key="y"),
    ]
)

train_formatter = neurad.pipeline.DataFormatter(
    {
        "x":None,
        "y":None,
    }
)

stream_kwargs=dict(
    transformer=train_transformer,
    formatter=train_formatter,
    transform_controls={},
    batch_size=batch_size,
)

There are quite a few parameters going in to the ensemble initialization but most of them won't differ between the examples we are looking at here so we might as well collect the shared parameters for convenience.

shared_kwargs = dict(
    source_identifiers=np.arange(len(x_train)),
    batcher_factory=neurad.pipeline.PermutationBatcher,
    train_stream_kwargs=stream_kwargs,
    validation_stream_kwargs=stream_kwargs,
    start_parameters=start_parameters,
    initial_dispersion=0.01,
    fold_seed=1234,
    perturbation_seed=4321,
)

We will begin with an "ensemble" of just a single model. Training the model in this way makes it easier to collect diagnostics. We can just use the base model for this ensemble.

mono_ensemble = CircularDiffusionMetaModel(
    model=base_model,
    n_folds=1,
    k_overlap=0,
    iterations_per_round=10,
    mixing_alpha=0.0,
    diffusion_on=False,
    **shared_kwargs
)

Unfortunately because the parameters for each optimizer aren't actually initialized until after the first training loop we can't simply use the same base model for each ensemble but instead we actually need to build and compile a fresh model per ensemble so that there are no data-leaks in the form of shared optimizer parameters (that was fun bug to figure out I can tell you).

The CPD models behave quite differently depending on how strongly you couple the parameters of the different models together via diffusion steps. Therefore I have made one strongly coupled ensemble, which should train quickly but which may have more poor data isolation properties, and one weakly coupled ensemble, which will train more slowly but which should have better data isolation.

cpd_sc_model = make_network(**model_kwargs)
cpd_sc_model.compile(loss="categorical_crossentropy", optimizer="adadelta")

cpd_sc_ensemble = CircularDiffusionMetaModel(
    model=cpd_sc_model,
    n_folds=10,
    k_overlap=3,
    mixing_alpha=0.5,
    iterations_per_round=10,
    **shared_kwargs
)

cpd_wc_model = make_network(**model_kwargs)
cpd_wc_model.compile(loss="categorical_crossentropy", optimizer="adadelta")

cpd_wc_ensemble = CircularDiffusionMetaModel(
    model=cpd_wc_model,
    n_folds=10,
    k_overlap=2,
    mixing_alpha=0.025,
    iterations_per_round=30,
    **shared_kwargs
)

kfolds_model = make_network(**model_kwargs)
kfolds_model.compile(loss="categorical_crossentropy", optimizer="adadelta")

kfolds_ensemble = CircularDiffusionMetaModel(
    model=kfolds_model,
    n_folds=10,
    k_overlap=8,
    mixing_alpha=0.0,
    iterations_per_round=10,
    diffusion_on=False,
    **shared_kwargs
)

test_transformer = neurad.pipeline.DataTransformer(
    [
        NumpyArrayTransformWrapper(x_test, output_key="x"),
        NumpyArrayTransformWrapper(y_test_onehot, output_key="y"),
    ]
)

test_stream = nrd.pipeline.DataStream(
    batcher=nrd.pipeline.FixedBatcher(np.arange(len(x_test))),
    transformer=test_transformer,
    formatter=train_formatter,
    transform_controls={},
    batch_size=batch_size,
)

Diagnostic Value Collection

I will focus mostly just on tracking classification accuracy of the various models on the different data sets. But every pairing of model and data set is of potential interest not to mention the performance of the mean model parameters. I thus compute the accuracy of every set of model parameters (including the global average parameters) on all of the training data folds individually as well as the test data. The large number of models combined with the large size of the test data set means that more time is actually spent evaluating the various model accuracies than is spent training the models.

On a larger real world problem you probably wouldn't want to use this sort of diagnostic collection as frequently as we are doing here since it would hugely explode your training time. Though it might be worthwhile to collect these diagnostics once at the end of a full training run for these type of model ensembles.

def collect_diagnostics(meta_model, test_stream):
    train_accs = []
    test_accs = []
    cv_accs = []
    acc_matrix = np.zeros((meta_model.n_folds, meta_model.n_folds))
    
    for model_idx in range(meta_model.n_folds):
        train_accs.append(meta_model.accuracy_on_stream(meta_model.training_streams[model_idx], parameters=model_idx))
        test_accs.append(meta_model.accuracy_on_stream(test_stream, parameters=model_idx))
        
        validation_idx = (model_idx - meta_model.k_overlap - 1) % meta_model.n_folds
        for data_idx in range(meta_model.n_folds):
            fold_stream = meta_model.fold_streams[data_idx]
            cur_fold_acc = meta_model.accuracy_on_stream(fold_stream, parameters=model_idx)
            acc_matrix[model_idx, data_idx] = cur_fold_acc
            if data_idx == validation_idx:
                cv_accs.append(cur_fold_acc)
    
    test_acc_centroid = meta_model.accuracy_on_stream(test_stream, parameters="average")
    
    diagnostics = dict(
        cv_accuracies = cv_accs,
        mean_cv_acc = np.mean(cv_accs),
        train_accuracies = train_accs,
        mean_train_acc = np.mean(train_accs),
        test_acc_centroid = test_acc_centroid,
        test_accuracies = test_accs,
        mean_test_acc = np.mean(test_accs),
        acc_matrix=acc_matrix,
        round_num = meta_model.n_diffusion_steps,
        gradient_num = meta_model.n_gradient_steps,
    )
    return diagnostics

Model Training

Instead of training for a certain number of passes through the data it is more meaningful to train each model ensemble for a certain amount of time. The monolithic model "ensemble" trains much faster than the rest of the models and so we only train it for a fraction of the total time that we train the other models so that the total number of training batches is similar between it and the other models.

run_duration = 50
n_runs = 40

fit_diagnostics_mono = []

for i in range(n_runs):
    stime = time.time()
    mono_ensemble.timed_training_run(run_duration/10)
    etime = time.time()
    achieved_duration = etime-stime
    cdiag = collect_diagnostics(mono_ensemble, test_stream=test_stream)
    cdiag["dt"] = achieved_duration
    fit_diagnostics_mono.append(cdiag)
    print(cdiag["gradient_num"]*batch_size/n_train, cdiag["mean_test_acc"], cdiag["mean_cv_acc"], cdiag["test_acc_centroid"],)

0.816 0.83256 0.8391 0.83256
1.872 0.8553 0.8622 0.8553
2.928 0.87578 0.8888 0.87578
3.968 0.88492 0.89885 0.88492
5.024 0.89202 0.90985 0.89202
6.064 0.8944 0.9171 0.8944
7.104 0.89716 0.92175 0.89716
8.144 0.90546 0.9347 0.90546
9.184 0.90598 0.9372 0.90598
10.24 0.90776 0.94105 0.90776
11.28 0.9101 0.9466 0.9101
12.304 0.91112 0.95165 0.91112
13.344 0.91136 0.95515 0.91136
14.368 0.90822 0.95565 0.90822
15.408 0.91482 0.9652 0.91482
16.448 0.91478 0.9693 0.91478
17.504 0.91028 0.96975 0.91028
18.544 0.91156 0.9698 0.91156
19.584 0.91396 0.9727 0.91396
20.64 0.91494 0.97895 0.91494
21.68 0.91466 0.98115 0.91466
22.72 0.91506 0.9834 0.91506
23.76 0.91536 0.9835 0.91536
24.8 0.9152 0.98735 0.9152
25.856 0.9129 0.98555 0.9129

fit_diagnostics_sc_cpd = []

for i in range(n_runs):
    stime = time.time()
    cpd_sc_ensemble.timed_training_run(run_duration)
    etime = time.time()
    achieved_duration = etime-stime
    cdiag = collect_diagnostics(cpd_sc_ensemble, test_stream=test_stream)
    cdiag["dt"] = achieved_duration
    fit_diagnostics_sc_cpd.append(cdiag)
    print(cdiag["gradient_num"]*batch_size/n_train, cdiag["mean_test_acc"], cdiag["mean_cv_acc"], cdiag["test_acc_centroid"],)

1.024 0.84569 0.8485 0.85178
2.064 0.86953 0.8796 0.87276
3.104 0.88149 0.89545 0.88494
4.128 0.890404 0.905 0.89364
5.184 0.89668 0.9175 0.89958
6.208 0.900268 0.9246 0.90462
7.248 0.904828 0.9358 0.90816
8.288 0.907316 0.9426 0.90988
9.328 0.909774 0.94665 0.9124
10.368 0.910686 0.9524 0.91332
11.408 0.911746 0.958 0.91488
12.448 0.913 0.9633 0.91522
13.488 0.912692 0.9676 0.91522
14.528 0.913554 0.9737 0.91684
15.568 0.913784 0.97695 0.91644
16.624 0.91467 0.9807 0.91668
17.664 0.913578 0.98225 0.9156
18.704 0.915182 0.98635 0.91698
19.744 0.915278 0.9891 0.91708
20.784 0.914284 0.99015 0.91618
21.824 0.914988 0.9918 0.91774
22.864 0.91501 0.9936 0.91666
23.904 0.915242 0.99505 0.91708
24.944 0.915216 0.9957 0.91636
25.984 0.914658 0.99615 0.91678

fit_diagnostics_wc_cpd = []

for i in range(n_runs):
    stime = time.time()
    cpd_wc_ensemble.timed_training_run(run_duration)
    etime = time.time()
    achieved_duration = etime-stime
    cdiag = collect_diagnostics(cpd_wc_ensemble, test_stream=test_stream)
    cdiag["dt"] = achieved_duration
    fit_diagnostics_wc_cpd.append(cdiag)
    print(cdiag["gradient_num"]*batch_size/n_train, cdiag["mean_test_acc"], cdiag["mean_cv_acc"], cdiag["test_acc_centroid"],)

1.152 0.837952 0.83725 0.82404
2.352 0.861276 0.86055 0.8535
3.552 0.86812 0.86895 0.8739
4.752 0.881922 0.8839 0.88356
5.952 0.88572 0.8857 0.89194
7.104 0.891414 0.89315 0.89708
8.256 0.895706 0.8948 0.90074
9.456 0.897668 0.89785 0.90242
10.608 0.899154 0.90085 0.90434
11.808 0.900334 0.90305 0.90744
13.008 0.899328 0.90335 0.90968
14.208 0.901854 0.9047 0.91064
15.36 0.903124 0.90895 0.91188
16.56 0.904408 0.9113 0.91208
17.76 0.902906 0.9106 0.91332
18.96 0.90553 0.9147 0.91436
20.16 0.906328 0.9193 0.91458
21.36 0.907208 0.92175 0.9152
22.56 0.905856 0.92445 0.91528
23.76 0.907976 0.9296 0.91542
24.96 0.907398 0.93325 0.91594
26.16 0.907112 0.9357 0.9149
27.36 0.908106 0.93815 0.91596
28.56 0.908084 0.94215 0.9159
29.76 0.908022 0.94465 0.91618

fit_diagnostics_kfolds = []

for i in range(n_runs):
    stime = time.time()
    kfolds_ensemble.timed_training_run(run_duration)
    etime = time.time()
    achieved_duration = etime-stime
    cdiag = collect_diagnostics(kfolds_ensemble, test_stream=test_stream)
    cdiag["dt"] = achieved_duration
    fit_diagnostics_kfolds.append(cdiag)
    print(cdiag["gradient_num"]*batch_size/n_train, cdiag["mean_test_acc"], cdiag["mean_cv_acc"], cdiag["test_acc_centroid"],)

1.024 0.839744 0.83815 0.8112
2.064 0.86176 0.86245 0.82854
3.104 0.872108 0.87355 0.83406
4.144 0.88547 0.8843 0.84924
5.184 0.8898 0.88905 0.84982
6.224 0.89602 0.89545 0.85112
7.264 0.898716 0.8958 0.85612
8.304 0.903832 0.90335 0.8547
9.344 0.904614 0.9048 0.85884
10.384 0.906166 0.9062 0.85782
11.392 0.907512 0.90865 0.85742
12.4 0.907744 0.9085 0.86088
13.408 0.909978 0.9108 0.85908
14.416 0.910182 0.9114 0.86076
15.44 0.910338 0.91025 0.8578
16.448 0.911348 0.91155 0.85778
17.44 0.912136 0.91225 0.85912
18.448 0.912682 0.913 0.85832
19.472 0.912772 0.91165 0.85736
20.48 0.912808 0.9127 0.8583
21.488 0.912952 0.91125 0.85512
22.512 0.91384 0.91455 0.85566
23.552 0.913362 0.9134 0.85306
24.592 0.912508 0.91085 0.85378
25.632 0.911828 0.91035 0.85498

mono_df = pd.DataFrame(fit_diagnostics_mono)
cpd_sc_df = pd.DataFrame(fit_diagnostics_sc_cpd)
cpd_wc_df = pd.DataFrame(fit_diagnostics_wc_cpd)
kfolds_df = pd.DataFrame(fit_diagnostics_kfolds)

for df in [mono_df, cpd_sc_df, cpd_wc_df, kfolds_df]:
    df["training_time"] = np.cumsum(df["dt"].values)

Training Speed

My initial goal was to make an ensemble training method which would have the data insulating qualities of K-folds but which would leverage message passing to get accelerated training. Did it work?

The answer depends on how closely you couple the parameters of the different models together and whether you are talking about speed or data insulating. As you can see below CPD with strongly coupled model parameters (an ensemble with a high $\alpha$) trains somewhat faster than the corresponding K-folds ensemble, both in terms of training time and in terms of increase in increased accuracy per training batch. But very weakly coupled CPD actually takes longer to train than a K-folds style model.

Unfortunately even in the case of the strongly coupled CPD the model takes longer to train in terms of wall clock time than simply training up a single model. Though if you are measuring model training in terms of number of training batches fed to each model CPD has a slight edge over training just a single model or training a K-folds ensemble. The fact that the K-folds and single model training curves are essentially the same when taken in terms of training batches per model is to be expected since the K-folds ensemble is just training the same model 10 times each with 90% of the same data.

model_diagnostics = [
    dict(df=mono_df, model_name="Single Model", color="k", linestyle="-"),
    dict(df=cpd_sc_df, model_name="CPD [Strong Coupling]", color="r", linestyle="-"),
    dict(df=cpd_wc_df, model_name="CPD [Weak Coupling]", color="r", linestyle="--"),
    dict(df=kfolds_df, model_name="K-folds", color="b", linestyle="-"),
]

fig, axes = plt.subplots(1, 2, sharey=True)

for mdiag in model_diagnostics:
    pl_kwargs = dict(data=mdiag["df"], label=mdiag["model_name"], color=mdiag["color"], linestyle=mdiag["linestyle"])
    axes[0].plot("gradient_num", "mean_test_acc", lw=3, **pl_kwargs)
    axes[1].plot("training_time", "mean_test_acc", lw=3, **pl_kwargs)

axes[0].legend()
axes[1].legend()
axes[0].set_xlabel("Training Batches per Model")
axes[1].set_xlabel("Time [seconds]")
axes[0].set_ylabel("Prediction Accuracy");

Global Average Parameter Performance

In the speed analysis we were comparing the average performance of the various models in the ensemble on the test data. But in CPD because we let the models communicate during training we can expect that the average model parameters over all of the models in the ensemble should be a valid model. Intuitively I would expect also the model corresponding to the global mean parameter set to behave better than any individual model in the ensemble.

Note that this is not the case for K-folds where I expect that because there is no communication between the different models the post-processing average of all the parameters in the k-folds ensemble is likely to be nonsense and so we should expect it to have significantly poorer performance than any model in the ensemble.

fig, axes = plt.subplots(1, 2, sharey=True)

axes[0].axhline(0.913, alpha=0.5)
axes[1].axhline(0.913, alpha=0.5)

for mdiag in model_diagnostics:
    pl_kwargs = dict(data=mdiag["df"], label=mdiag["model_name"], color=mdiag["color"], linestyle=mdiag["linestyle"])
    axes[0].plot("gradient_num", "test_acc_centroid", **pl_kwargs)
    axes[1].plot("gradient_num", "mean_test_acc", **pl_kwargs)

axes[0].legend()
axes[1].legend()
axes[0].set_title("Accuracy at central parameters")
axes[1].set_title("Typical model Accuracies")

for ax in axes:
    ax.set_xlabel("Training Batches per Model")

axes[0].set_ylabel("Prediction Accuracy");

When dealing with the average parameters both the strong and weakly coupled CPD outperform the typical accuracy of one of the models in their ensemble (as expected) and k-folds gets a significant hit in performance when we try using the mean model parameters (as expected). Note that the fact that the K-folds mean parameters performs better than random is due to the fact that we started all of the models int he K-folds ensemble at very nearly the same point in parameter space, something which is not usually done for K-folds.

I find it very interesting that in the case of the weakly coupled CPD ensemble the test accuracy of the centroid parameters roughly follows the typical accuracy curve of the single model trained with all the data. The fact that the performance of each model in the weakly coupled CPD is relatively poor suggests that the models have failed to effectively communicate with each other. If the models are allowed to drift too much apart then we would expect a decrease in performance from taking the average parameters just as in the case of K-folds. But, apparently even though the communication has been too weak to much heighten the performance of the individual models, it has been somehow strong enough to keep the different models compatible with each other.

I want to emphasize the importance of the fact that we can replace the CPD ensemble with a single model and still get an increase in performance, which is a very significant advantage over a K-folds type ensemble. A K-folds trained ensemble may give better predictions than any single model in the ensemble when the models are somehow allowed to vote. but this requires keeping around and deploying K different models instead of just 1 which is usually not worth the headache.

Data Isolation

So a CPD ensemble trains slightly faster than a K-folds version, but instead of having perfect isolation of some data from the parameters of some models we have just an approximate isolation, and one that we can only expect to get worse over time.

We can test the degree of information leakage between each data fold and each model by comparing the accuracy of the model predictions on that data fold and the accuracy of that model on the test data. In the case of K-folds there is no communication at all between models and so there is no information leakage from the held out data folds and the associated models. In CPD although there are no data folds which are perfectly isolated there are data folds which take a larger number of diffusion steps to reach the parameters of a given model. In the early stages of training we should expect that the maximally isolated data folds should still act as being essentially independent validation sets. The more strongly coupled the model parameters are to each other and the more diffusion steps we have undergone the more likely that we are to have begun overfitting each model to even the most distant data fold.

fig, axes = plt.subplots(2, 1, figsize=(12, 8), sharey=True)

for mdiag in model_diagnostics:
    df = mdiag["df"]
    pl_kwargs = dict(lw =3, label=mdiag["model_name"], color=mdiag["color"], linestyle=mdiag["linestyle"])
    axes[0].plot(df["gradient_num"], df["mean_train_acc"]-df["mean_test_acc"], **pl_kwargs)
    axes[1].plot(df["gradient_num"], df["mean_cv_acc"] - df["mean_test_acc"], **pl_kwargs)

axes[0].legend()
axes[1].set_xlabel("Training Batches per model")
axes[0].set_ylabel("Overfitting \n Core Training Data")
axes[1].set_ylabel("Overfitting \n Maximially Isolated Data");

This all makes a lot of sense. The degree to which all the models predict the labels of the samples whose gradients they were fed directly increases with time. The larger the data set the longer it takes to overfit to. The single model which was fed all the training data with no distinction learns to overfit to all N training samples just slightly slower than the K-folds models overfit to their $(K-1)/K*N$ training samples. The strongly coupled CPD ensemble is the model that most quickly learns to fit the data and so it comes as no surprise to me that the higher training rate also comes with faster overfitting. Also because this higher training speed comes from frequent and strong parameter diffusion the models in the strongly coupled CPD also rapidly overfit to the data outside of the footprint of their immediate training data.

The weakly coupled CPD tells the most interesting story here. Each model in the weakly coupled CPD has access to only a very small subset of the total data and so it learns to overfit to that individual data set very quickly. However because the coupling between models is weak it takes a long time for the information about distant training folds to diffuse out to permeate the parameters of the models in the ensemble.

Diffusion Plots

An interesting new diagnostic that CPD makes possible is that we have much more information than simply the performance of our models on a hold out set and our training set to gauge how our models are fitting/overfitting to the training data. Because some models are more insulated from some data folds than others we can see a continuous progression from most overfit (the data on which each model trains directly), to most isolated.

fig, axes = plt.subplots(1, 3)

for mod_idx, mdiag in enumerate(model_diagnostics[1:]):
    df = mdiag["df"]
    im = axes[mod_idx].imshow(df["acc_matrix"].iloc[len(df)-1], vmin=0.9, vmax=1.0)
    axes[mod_idx].set_title(mdiag["model_name"])

cbar = plt.colorbar(im, ax=list(axes), orientation="horizontal", fraction=0.05)
cbar.set_label("Prediction Accuracy")

for ax in axes:
    ax.set_xticks(np.arange(10))
    ax.set_yticks(np.arange(10))
    ax.set_xlabel("Data Fold")
    ax.set_ylabel("Model Fold")

fig, axes = plt.subplots(1, 3)

for mod_idx, mdiag in enumerate(model_diagnostics[1:]):
    df = mdiag["df"]
    acc_matrix = df["acc_matrix"].iloc[n_runs-1]
    test_accs = np.array(df["test_accuracies"].iloc[n_runs-1])
    overfitting_matrix = acc_matrix - test_accs.reshape((-1, 1))
    im = axes[mod_idx].imshow(overfitting_matrix, vmin=0.0, vmax=0.1)
    axes[mod_idx].set_title(mdiag["model_name"])

cbar = plt.colorbar(im, ax=list(axes), orientation="horizontal", fraction=0.05)
cbar.set_label("Overfitting (Excess Accuracy)")

for ax in axes:
    ax.set_xticks(np.arange(10))
    ax.set_yticks(np.arange(10))
    ax.set_xlabel("Data Fold Index")
    ax.set_ylabel("Model Index")

Looking at the plots above we can see the different sorts of data insulation behaviors. With K-folds the accuracy is flat within the training footprint for each model and there is no leakage of information into the folds outside of the training footprint (as indicated by the accuracy being close to the test data accuracy).

In contrast the strong coupling CPD training shows uniform overfitting of all models to all data folds regardless of which data sets are being fed directly into which models.

The weak CPD is somewhere in between the two with high overfitting on the training footprint of each model and a slow fall off as we move to more weakly coupled models in the ensemble.

Final Thoughts

The version of CPD that I have put together in this post is potentially useful as it stands. However I suspect that this task is more susceptible to roughly linear models than many problems would be and that may be exaggerating the apparent success of the diffusion steps and the usefulness of the parameter centroid. Also because the speedup over a more traditional K-folds type training is only modest this sort of approach is unlikely to be useful anywhere that K-folds wouldn't be also an option. Potentially a parallelized version of CPD that is designed to run on many compute nodes in a cluster could potentially outperform the typical sort of parameter averaging approaches since the communication between nodes is completely scalable with no need for a central parameter server and is just one way. In addition as the success of the weakly coupled CPD shows it is possible to extend the number of gradient updates in between diffusion updates by decreasing the mangitude of the mixing parameter. These two properties together make CPD potentially very useful for scaling up to distributed training on large clusters.

Although CPD showed some training speedup in the strong coupling case in terms of training multiple models the strong coupling effectively destroyed the usefulness of the models as an ensemble and so I would have to say that using either K-folds or just training a single model with all the data is probably a superior option. The increase in model performance in this case that we got from using the central parameters of the ensemble is probably mostly just due to effectively smoothing some of the noise out of the parameter updates from the different models. I wouldn't be surprised to find that taking a temporal running average of the model parameters behaves similarly to the centroid parameter performance in the strongly coupled case.

I think that weakly coupled CPD could be potentially a very powerful tool if an effective means can be found to keep the information leakage slow without completely stifling inter model communication. Using a very low mixing rate works fine but also makes the models communicate very ineficiently and so again ultimately a K-folds type CV is probably the way to go if maintaining data isolation is a must. But there are other potentially interesting ways to go about maintaining data isolation that I haven't explored yet. Uppping the noise in each model from regularization is a promising strategy. The coupling of the models together allows the training to benefit from a higher level of noise in the individual parameter updates than might be the case when training just a single model alone. Higher noise in the updates in turn should somewhat slow communication via diffusion. Intuitively anything that slows overfitting on the training set, like data augmentation, or l2 coefficient regularization, etc, ought to slow information leakage between models training on adjacent data folds. Trying to tweak the regularization mix to keep information leakage small seems more directly related to the goal of good generalization than simply searching over a hyper parameter grid to find the dropout rate which performs best on the hold out set. I think balancing data leakage and regularization strength is a beautiful way to approach model regularization but that doesn't necessarily mean it is a good way to approach it in practice.